なんらかの理由でこのサイトのシステムはタイトル名の漢字は中国語の発音にする。ローマ字にするときに何らかのプロセスがあるみたい。僕はつまらない人間ですね。全身脱毛はしないけど。別にそう言う人たちはつまらないの意味合いではない。この投稿はノンセンスだ。
Archives: 2024
シンメトリ
I
♥
YOUOY
I
♥
U
I,♥,U はシンメトリがある文字、他のもみつかりますか。
ここはも一つの概念みたいのこと。 あれはシンメトリという概念。 これも数学と理学に大事な概念の一つ。 世の中すべてはシンメトリがあるとは分からないけど。 シンメトリ=美しい とか シンメトリ=パーフェクト ということは分からない。 そういうわけでもないと思うけどそういう風に考える人もいる。 でもシンメトリがあるだから"便利"だ。
例えば
- 数字には-と+もある。 -2,-1,0,1,2
- 形(shapes) はシンメトリの線がある。(全部じゃないけど〜) など。
ここでは説明が足りないかも。上手く説明出来なかった本当にすみません。
シンメトリにかんしてのだいたいの理解でした。
About Christmas
How did you celebrate your Christmas Eve? Did you stay awake the whole night waiting for Santa Claus to come? Or did you go straight to bed after your Christmas dinner hoping to find some presents when you wake up the next morning?
For some people Christmas is about the presents that they get. For some it's about the dinner they have with their family. For others it's about the songs and the festive mood. There are those who only think of it as a holiday. And there are also those who go to church to pray.
How was my Christmas Eve? Nobody invited me to celebrate with them. Will you invite me to your Christmas dinner next Christmas?
Verbs
- stay [stayed, staying]
- awake [awoke, awaking]
- wait [waited, waiting]
- find [found, finding]
- think [thought, thinking]
- pray [prayed, praying]
- invite [invited,inviting]
∞
∞ は 数字 ではない。
- ∞ は
- 概念見たいなことだ。無限。
- シンボル、特別なシンボル。
- 数えられない数字、数字でもないけど一番大きい数字より大きい。
数学にとって大事な概念。役に立つな概念。
数学分野(または理学)の使い方と日常(エンタメとか)のは少し違うかも。専門家は怒るかも。 でもこれは仕様がないのことだ。日常のほうが多い。子供は専門家になるまえには大丈夫。専門家の前には気をつけなさい。
本当はこれより難しいことけど子供に説明ときとか分かりやすいためにはいいかも。
僕のだいたいの理解でした。
Number Line

例えば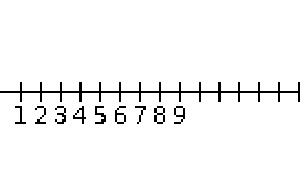
≒と≈
≒ と ≈ は だいたい おなじ の いみ は どこで きいた や よんだこと は おぼえていなかった。どこだったんだ。
シンボルということは分野によることなることもある。こどもにはわかってもらうことはシンボルをつかうまえにシンボルのいみをかくにんすること。だいたいていうことは。。。だいたいというがいねんにかんけいがある。
だいたいのがいねんはべつのはなしにしましょう。
ちがうシンボルのりゆうはたぶんほんのフォントにかんけいがある。しゅっぱんしゃがつかったフォントとか当時の技術にできること。また当時は情報の発信や分野の交換はいまと違うから。あとにんげんはシンボルをつくるのがとくい。たまにひつようせいがあるだから。たまにたのしいやおもしろいだから。だいたいそいうかな。
>と< の つづき
<と> の ほかにも ≤ と≥ もある
>と< の ほかにも ≥と≤ も ある (もしこちの表情のほうがいいと思うの)
Estimation は 適切なタイトルかどうか分からないけど。関係せいがあるからこのタイトルで行こうかな。Estimationは子供にとって役に立つと思う。"だいたい" と言う概念は役に立つと思う。人間の知識はだいたいのもんと思わない?僕の知識もだいたいのものだ。全部のことは知らない、すべて分かるのでもない。ある程度分かる。ある程度理解できる。だいたい。。。
では 前回のEstimationの続きの続き。
=、>、< の あと は ≥ と ≤ (この順番ではなくても大丈夫)
≤ (あるいは <= ) は < プラス = の 意味
≥ (あるいは >= ) は > プラス = の 意味
例えば
- x≤8 は 8より小さな数字、でも8も含めている
- x≥8 は 8より大きな数字、でも8も含めている
数字は1、2、3、4、5、6、7、8、9、10、11なら
- x≤8 は 1、2、3、4、5、6、7、8だ
- x≥8 は 8、9、10、11だ
(数字って数字の線、Number Lineって言うこと)
ちなみにプログラミング言語(例外もあるけど)で ≤ は( <= ) で書いていて ≥ は( >= )で書いている。キーボードにはそれがないから。
実は ≱ と ≰ と ≯ と ≮ と ≠ も ある。「じゃない」という意味。 でも論文以外にあまり見たことないと思う。
あと だいたい の しるし は ≒ と ≈ もある。ほかにもあるらしい。
>と<と ≒や≈はどの関係か。あれは"だいたい"こんな時かな。
0.99999999 <X<1.0000001 は X≈1 の 時もある。だいたい。 だいたい。。。
(関係性はすぐじゃないけど。だいたいと言う概念はものを買うの時に値段を見る時とか物の数とか量などにも子供に気づいてもらえると思う)
だいたいの概念。だいたい分かる。(独り言は難しい!〜) (自己アピールも苦手!)
あいのしるし© 2024
難しいこと
独り言が難しい、 反応がない、 役に立つかどうかも分からない。
Estimationの続き
前回の Estimation(仮のタイトルそのまま。。。)の続きだけど。 このタイトルも仮です。。。
日本の学校はこういうのも習うが分からないけど。今回のは少しシンプルだけど。
Number Lineって言うこと。
例えば 0から10まで
0 1 2 3 4 5 6 7 8 9 10 (これは絵で表示する方がいいかも)
ここに使ったのはIntegersって言う数字タイプ(種類) この段階で数字のタイプ(種類)を話すのは子供の興味によるかも。 IntegersだけではなくFractions(Fractional Number),Decimal Numberなどもある。 どっちを使うのは場面によって。数字はものを数えるためという考えもあると思う。 だからどんなタイプを使うのはなにを数えるとかどれぐらいの正確が必要とかなどを考える。 日常生活に使う数字と研究場に使う数字には正確性やレンジ(どこからどこまで)の違いがある。
上の 0から10まで の Number Line で 数字の大きさ や 順番 を 分かる、見られる。
ここで 0から10までに X>5 の は 6、7、8、9、10 のこと を分かる。 あと X<8 は 0、1、2、3、4、5、6、7 だ。
いろいろなことが聞ける。
- 6と9どっちが大きいなども子供に聞ける。
- 1と10どっちが8に近いとか。
- Xはなんですか。 X>8とX<10
- X>0とX<5はなに。
- 6より大きい数字けど9より小さい数字は>と<を使ってそれを示すこと。
(これで子供の理解をチェックすることができると思う、数字の順番、など)
0から10までには簡単だけどNegative Integersを習う時には多分役に立つかも。
あと順番のこと。基本敵には(ascending)小さいから大きいまで と(descending) 大きいから小さいまで。
(ここで説明の限界があると思う、何かもの足りないの感じだ)
Estimation (>と<)
Estimation (タイトルは仮のもの)
ここは 推計とか算定 の 意味かな
子供には数字を計算でも算定(この言葉が適当か分からないけど)ができればいいと思う。
まず は > と < を馴染めること。 = の しるし 以外にも >と< の しるし もある。
あと ≒とか ≈など は だいたい の しるし (22日12月に追加)。
a > b 左がわの a は 右がわの b より 大きい
b < c 左がわの b は 右がわの c より 小さい
a,b,c は 仮のもの、本当は数字 とか 数学 の Algebra の シンブル。 数学にあるa,b,cはシンブルとして使えるから英語のa,b,cとはちょと違う。ふだんaはbより大きいということはない。子供に分かってもらえる。(ここは意見の違うこともあると思う。数学はある程度建物のように段階てきに重ねることと思うから最初から重要な基礎や知識を教えてほうがいいと思う。理想のは子供に合わせて教えることだから子供の反応やフィードバックが必要です、ここは難しいだから物足りない部分もあると思う。)
例えば 数字で
1<2 2>0
ここで 10 と 100 どち が 大きい とか 6 x 8 と 7 x 9 どち が 大きい など も ドリル に なれる。
ここのポイントは子供に > と < の 意味 や 使え方 を 馴染めること。そこで推定や算定のことを気づいてもらえる。